Selain dalam bentuk bilangan biasa , dalam bentuk aljabar juga terdapat yang namanya pecahan aljabar . Bagaimanakah cara untuk menyelesaikannya ? apakah sama prinsipnya dengan pecahan biasa ? ataukah berbeda ?
Diantara kita masih banyak yang beranggapan ketika mendengar kata aljabar bayangannya pasti sulit dan pasti membosankan . Apalagi ada tambahan kata pecahan , ini bagi sebagian orang pasti sudah takut terlebih dahulu dan bayangannya bahwa bentuk hitung ini sangat sulit dan rumit .
Untuk itu , mari kita pelajari bersama bagimana cara memecahkan operasi hitung pecahan aljabar supaya mudah untuk diselesaikan dan supaya anggapan – anggapan mengenai matematika itu sulit dan membosankan dapat kita rubah menjadi matematika itu mengasyikkan .
Dan sesungguhnya apabila kita cermati secara saksama , operasi hitung bentuk biasa dengan bentuk pecahan itu sama tidak ada bedanya . Jadi ,dengan kata lain kita harus fahan terlebih dahulu mengenai operasi hitung dasar . Operasi hitung dasar yaitu penjumlahan , pengurangan , perkalian , dan pembagian . Setelah kita memahaminya , maka tinggal kita aplikasikan ke dalam bentuk yang lain atau kali ini ke dalam bentuk pecahan aljabar .
Operasi Hitung Pecahan Bentuk Aljabar
Seperti dalam pecahan bentuk biasa , dalam pecahan bentuk aljabar juga ada 4 operasi hitung yaitu :
- Penjumlahan pecahan bentuk aljabar
- Pengurangan pecahan bentuk aljabar
- Perkalian pecahan bentuk aljabar
- Pembagian pecahan bentuk aljabar
Untuk lebih jelasnya , perhatikan penjelasan di bawah ini :
1. Penjumlahan Dan Pengurangan Pecahan Bentuk Aljabar
Untuk menyelesaikan pecahan bentuk aljabar , prinsipnya sama dengan menyelesaikan penjumlahan pecahan biasa yaitu dengan cara menyamakan penyebutnya terlebih dahulu baru di jumlahkan atau dikurangkan .
Perhatikan contoh – contoh di bawah ini :
- Sederhanakan benuk pecahan aljabar berikut
Penyelesaian:
- Selesaikan bentuk pecahan aljabar berikut ini :
Penyelesaian :
Dari contoh – contoh diatas ,dapat kita simpulkan bahwa ketika akan menyelesaikan operasi hitung penjumlahan dan pengurangan kita lihat terlebih dahulu penyebutnya . Jika sama , maka langsung kita jumlahkan atau kurangkan . Namun , jika berbeda penyebutnya maka kita samakan terlebih dahulu baru kita kurangkan atau jumlahkan . Atau dengan kata lain prinsip penyelesaian operasi hitung pecahan biasa dan pecahan aljabar sama .
2. Perkalian Dan Pembagian Pecahan Bentuk Aljabar
a. Perkalian Pecahan Bentuk Aljabar
Cara untuk menyelesaiakan operasi hitung pecahan bentuk aljabar prisnsipnya sama dengan perkalian pecahan bentuk biasa . Yaitu dengan cara mengalikan pembilang dengan pembilang dan mengalikan penyebut dengan penyebut .
Rumus :
Untuk lebih jelasnya , perhatikan contoh di bawah ini :
- Sederhanakan perkalian pecahan bentuk aljabar berikut
Penyelesaian :
b. Pembagian Pecahan Bentuk Aljabar
Untuk menyelesaiakan pembagian pecahan bentuk aljabar , caranya sama dengan menyelesaikan pembagian pecahan biasa , yaitu dengan cara merubah ke bentuk perkalian dimana bilangan kedua dibalik, penyebut menjadi pembilang dan pembilang menjadi penyebut .
Rumus
Supaya lebih jelas lagi , perhatikan contoh di bawah ini :
- Sederhanakan bentuk pembagian pecahan aljabar berikut :
Penyelesaian:
3. Perpangkatan Pecahan Bentuk Aljabar
Perpangkatan yaitu perkalian perulangan bilangan dengan bilangan yang sama . Hukum ini berlaku juga dalam bentuk pecahan aljabar .
Rumus :
Untuk lebih jelasnya , perhatikan contoh berikut ini :
- Sederhanakan pecahan bentuk aljabar berikut :
Penyelesaian :
Demikian penjelasan mengenai operasi hitung pecahan bentuk aljabar . Mudah bukan ? inti dari pecahan aslinya sama yaitu ketika dijumlahkan atau dikurangkan maka penyebutnya harus sama . Dan apabila akan di bagikan maka rubah ke dalam bentuk perkalian dimana penyebut dan pembilang di bilangan ke dua di balik . Dan ketika mengalikan bentuk pecahan tinggal dikalikan penyebut dengan penyebut dan pembilang dengan pembilang . Dan ketika menyederhanakan bentuk pecahan ketika sudah tidak memiliki faktor yang sama kecuali 1 . Atau seperti yang telah di contohkan di atas .
Inti dari operasi hitung diatas adalah harus menguasai operasi hitung penjumlahan , pengurngan , perkalian ,pembagian , perpangkatan serta memahami apa itu FPB atau memahami faktorisasi dari kedua pecahan yang sedang di hadapi atau yang akan diselsesaikan .
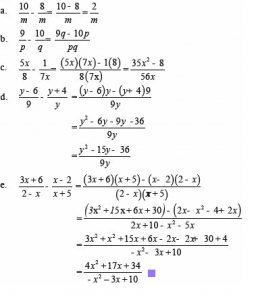
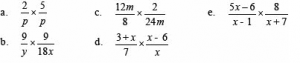

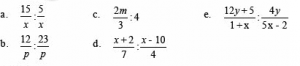

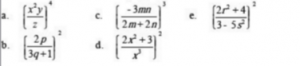

No comments:
Post a Comment